Paper Plate Education
"Serving the Universe on a Paper
Plate"
We recommend you visit Bradford Hansen-Smith's pages at www.wholemovement.com

 Explore the work of
Explore the work of
·
The
circle
·
Geometry
·
History
·
Requirements/materials
·
Folding
circle in half
·
Principles
·
Folding
3 diameters
·
Make
a sphere
·
Make
a tetrahedron
|
|
·
Make
an octahedron
· Make an icosahedron
·
4-frequency
diameter grid
·
8-frequency
diameter grid
·
4
and 5 diameter fold
·
Books
·
Photos
of models
· Contact
The circle
The paper plate is a circle. The circle is
fundamental to everything we know. Consider that we have drawn pictures of
circles for over two thousand years. To get information from this static image
we’ve had to invent sophisticated construction methods, using parts of circles
(points, arcs and straight lines). The circle is just one of endless shapes used
in art. In philosophy it is a symbol for everything. In math it is zero, a
symbol for nothing. The image is used for many diverse purposes, representing
ideas and concepts of all kinds. Practical uses of the circle have been
excessively explored. We know very little of the information held within the
circle.
The nature of Wholeness is demonstrated in the circle
shape. The circle in space is dynamic, it moves and can generate information in
a way not other shape can do. Countless forms and endless systems of spatial
complexities can be made by folding and joining circles. This process reveals
fundamental 2-D and 3-D mathematical information through divisional movement
without separation. The patterns and formations of interrelated systems that
come from reconfiguring the circle are the same as those observed in natural
phenomena, pattern source for all areas of human understanding.
This approach to the circle is spatial, a concrete forming of patterns. Complexities of transformational movement systems are developed from a simple, sequential process of folding. It shows forms changing one into another. Complexity of form is a function of the circle in multiple reflection, generating things that would be very difficult to model in other ways.
Geometry
The word geometry means earth measure. “Geo”
means earth, the earth is spherical. The sphere is the only form we know that
inherently demonstrates the concept of the Whole. “Metry” is about
measure, intervals of movement between any two locations. The word
geometry then comprehensively means Wholemovement, movement of the Whole
to itself. Context is what gives meaning to anything. The greatest context gives
the greatest meaning. The greatest meaning of geometry is then Wholemovement.
The greater context of the circle is the sphere.
The circle is a compression of the sphere to a flat
plane. The sphere does not lose
anything, it is simply compressed, reformed to a circle disk in space. Through
the folding movement of the circle all spherical information can be retrieved,
unfolded if you like.
We all started from a singular spherical egg cell. Through division of this singular sphere we came into this huge time/space sphere. Our experience is the movement between, the scaling of a spherical Whole beyond understanding. The circle is as large as it is infinitely small. That means the circle does not have a center, that is a scale function of concentricity. The circle is the center.
The Whole is self-referencing, nothing can be added
or taken away. It can only generate and reflect, through movement, the wholeness
of what it is. Many paper plates are used, each
reflecting the other. The paper plate circle is never cut. To cut
the circle is to separate into parts, limiting ourselves to individual
boundaries of endless fragments. This is also wasteful.
History
Folding circles has no history. There are no
references for folding the circle as a modeling tool or as a process for
generating information. Most of mathematics is based on drawing pictures, using
the circle to mean what ever we favor to think at the time. We continue trying
to explain this time/space location
of movement patterns ordered to the Whole of what is, in abstractions drawn from
static circle images that have been separated into parts and removed from their
context.
The only historical reference I have come across is
that in Japan in the late 30’s and early 40’s they were folding circles as
well a squares. Somewhere in the history of origami lies the circle,
unrecognized. The square and all other polygons are only a part of the circle,
therefore limited to specific number of sides. The circle has no sides, it is
without limit, without scale.
After ten years of intensive exploration into
geometry, I realized everything we know about patterns are divisions into a
sphere. The sphere compressed is a circle. Nothing of the sphere is lost. How
then to reveal it? I have been folding paper plates for twelve years
decompressing information. I find new things all the time. Students show me new
things. It is an endless process.
Requirements/materials
There is no age or educational experience required.
Any one who can fold a paper plate in half can do it, from 5 years old on up.
Paper plates, masking tape and bobby pins are used. There is no cutting or
measuring, only proportional folding of the circle. Coloring is another activity
requiring markers or paint. Glue can be used before taping. When glue is dry,
remove tape. Be as accurate as possible when folding points together, lines will
then be in correct place. Simple.
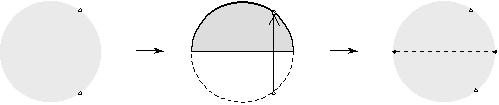
Folding circle in half
Unity
is not broken by folding the circle. Any two points on the circumference of a
circle, (imagined or marked) when touched together will fold the circle in half,
forming two new points on the circumference, 4 points total. The diameter is
perpendicular, half way between the direction of movement of the two points. By
this action of symmetry a tetrahedron pattern is formed (4 points in
space is a tetrahedron pattern; 3 sets of 6 edges where opposite directions are
at 90° to each other) This right angle triangulated movement is principle to
all pattern formation. It happens first. This first movement shows a ratio of
1:2, one Whole (singularity) in two parts. It models the tetrahedral pattern of
Carbon, indicating the importance of this pattern as structural to the endless
development of life formation.
![]()
Principles
What
happens first? What are the qualities of this first movement? We start with the Whole
of the circle. Through self-referential movement a division occurs
revealing duality that takes the form of triangulation where each
aspect is consistent to the movement of the whole, and each individual
part is interdependent to the Whole, which then determines the interrelationship
between parts. I call these qualities principle. They are primary to everything
else the circle will do. They are principle directives reflected in all
movements and in all parts of the circle. What we determine to be principle is
the most reliable guide we have to direct our intentions beyond the conditional
mind. Others may interpret different qualities in that first fold. I have taken
what I find to be the most general, the biggest things that can be talked about.
The greater understanding of what is principle reveals the greatest potential
for meaningful action.
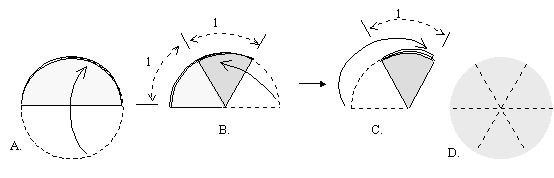
Folding 3 diameters
A.
Fold circle in half.
B.
Fold one corner point over making 2 equal
parts. Don’t measure, use your eyes to see the proportions correctly.
Our eyes are a proportional feed back systems designed to do just this type of
thing. Use them.
C.
Fold unfolded part behind and even up points and edges. Crease only when
the edges, points and circumference are even. One fold on top, in middle, and
one on the bottom, like a “Z”.
D. This
folds the semi-circle into thirds. Open to find 3 diameters.
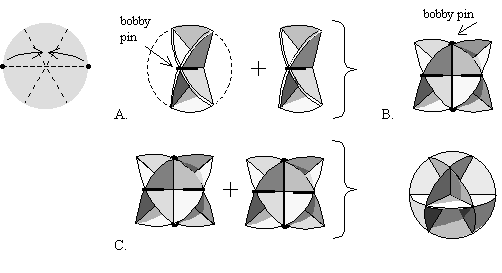
Make a sphere
A.
Bring 2 end points of one diameter together, hold them closed with a
bobby pin. This forms a pattern of 4 tetrahedra; 2 tetrahedra and 2 tetrahedral
intervals. Six points in space.
B.
Bobby pin 2 of these folded circles together in the same way, on the
straight edges showing a square, or quadrilateral pattern that moves on
perpendicular axis, reflecting first fold of circle.
C. Join 2 sets of 2 together, straight edges joined with bobby pins. This makes a sphere of open triangles and squares, a Vector Equilibrium, traditionally called a cuboctahedron. There are 13 points of intersection reflecting the number pattern of the hexagon, of which there are 4 (1+3=4) circles, each starting with 4 points.
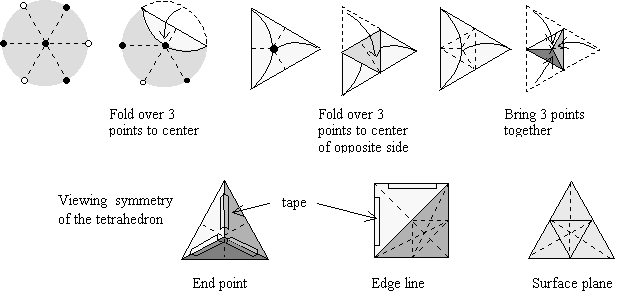
Fold 3 diameters into the circle. Fold 3 alternate
points on circumference (ends of diameters) to the center point. Crease well.
This forms a 2-frequency equilateral triangle.
Fold each end point of the triangle to the mid point
on the opposite side. Do all 3 points separately. Do not overlap these folds.
Crease well each fold with a straight edge. Bring end point together forming a
tetrahedron. Tape along edges to hold together.
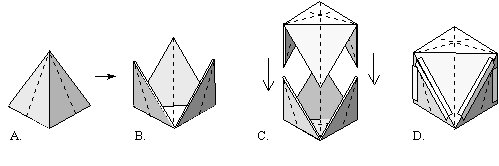
Make an octahedron
A. Fold
a tetrahedron as accurately as you
can.
B. Open
it half way so the triangular spaces are the same size as the triangles that
form them. There are now 6 points and 8 triangular planes; an octahedron
pattern.
C. Make
another tetrahedron and open it the same way. Join the 2 opened tetrahedra,
fitting the triangles of one into the triangle intervals of the other, joining
edge to edge.
D. Tape
together the full length of each
edge joining. This forms an octahedron.
You have now made a sphere with triangles and square
intervals, as well as two formed polyhedra. Both with triangles and one with a 3
squares relationship of triangles. These 3 formations are components to a single
system where all relationships are congruent, edges, surfaces and intervals.
They were all made from the same diameter circle.
There is a tremendous amount of exploration that can
be done by combining in various ways the vector equilibrium, the tetrahedron and
octahedron. The tetrahedron and octahedron are formed by 9 creases in the
circle, the tetrahedron folding. There are countless ways of reconfiguring and
joining the circle using only these 9 folded lines. Another example follows.
Make
an icosahedron
An icosahedron has 20 equalaterial triangular sides. By
using 4 tetrahedron you can make an icosahedron. Each tetrahedron when open
shows 4 equailaterial triangles, that is 16 equailaterial triangle in all; 4
short of the 20 needed to make the icosahedron; yet it can be done. You
have, in the circle, all the information you need to do this. Keep in mind these
are spatial patterns, form is simply a way to reveal patterns. Space is where
all the interconnections take place.
Good luck. Let me know how you do with this. (If you
can’t get it, I will send you instructions.)
By completing the icosahedron, you will then have
made the third primary polyhedra by folding only the tetrahedron. The other two,
the cube and the dodecahedron, can also be demonstraed by adding more tetrahedra,
stellating the faces of each, then stringing the points to show the form.
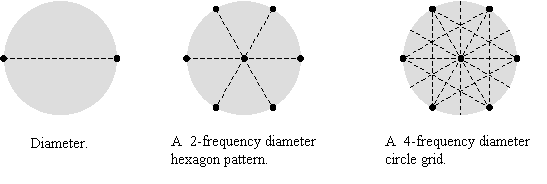
4-frequency
diameter grid
Everything starts with the 3 diameters, the hexagon pattern, 7 points. To increase the frequency of the diameters is to form the relationships of the 7 points. There are 42 specific combinations of relationships (7x6=42). That is about numbers, it does not tell us anything about the enormous potential of possible combinations of spatial configurations. To give form to these relationship we have to touch each point to all the others, fold and crease. In fact all we have to do is to make 9 folds to show all 42 relationships.
To make it simple: each of the 3 points on one
diameter when touched to one another will generate 3 parallel lines dividing the
diameter into 4 equal sections. By doing this to all 3 diameters, an equilateral
triangular grid is formed that serves as matrix for many levels of complexities
and generates tremendous amounts of mathematical information.
8-frequency diameter grid
The 8-frequency diameter grid circle is extending the same process of touching points to accurately divide each segment of the 3 diameters in half again. The 2 end points of each of the first 3 diameters, (not to be confused with the new 3 bisecting diameters, they are divided to a different proportion) will now be touched to the 2 new points of intersection on each diameter. These twelve new folds reveal the hexagon star of 3 diameters to be primary to an infinite equilateral triangular grid. This process of dividing the 3 diameters into higher frequencies (1:2 ratio) can be taken as far as your paper circle is large, and as your accuracy of folding allows.
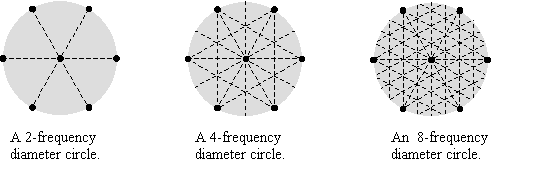
The 8-frequency diameter grid is much like an octave
in music, from which you can configure endless musical scores. Also like music,
the difference is in the intervals between the notes.
4 and 5
diameter fold
Once you have the circle folded in half, there are only 3 ways to again fold it in a ratio of 1:2. Remember, consistency is a directive principle to pattern development. This can be worked out with numbers, by traditional construction methods, or simply by proportionally folding the circle. Folding 3 times (1:2) gives 3 diameters, as we have seen. Folding 4 times to the same ratio generates 4 diameters and doing the same 5 times (1:2) reveals 5 diameters. The 3 diameters happen first and are therefore primary to the other two proportional folding. Once you understand the process of the development of the 3 diameters it is exactly the same for the 4 and 5. The forms will be differently proportioned since the diameter remains consistent and the distance on the circumference changes. The 3, 4, and 5, within the 6 are primary to understanding all spatial pattern. It is all without cutting or measuring, simply proportional folding of the circle.
Books
The Hands on
Marvelous Ball Book, Bradford Hansen-Smith. Hard
bound, 48 pages, full color, story, how-to-book.
Scientific American Books for Young Readers, W.H. Freeman Inc., NY, 1995
ISBN 1-887229-24-8
Price $16.95
This book is recommended for 5 year to about 9 or 10
years old. It is a good start in the process of folding and joining circles. It
is in a story format about Wholeness and why we use the circle.
The Geometry of
Wholemovement: folding the circle for information,
Bradford Hansen-Smith. Soft bound, 223 pages, black and white illustrated
how-to-book. Wholemovement Publications, IL, 1999
ISBN 0-7167-6628-0 Price $30.00
This book is comprehensive to the process. It will go
as far and as deep as you want to take it.
Both of these books can be ordered through Bradford Hansen-Smith, contact below.
Photos
These photos show models made from 9”diameter paper plates, during 1997-1999. They are
taken from the book The Geometry of Wholemovement: folding the circle for information

|




Contact
Bradford
Hansen-Smith
or
(773)
794-9764

